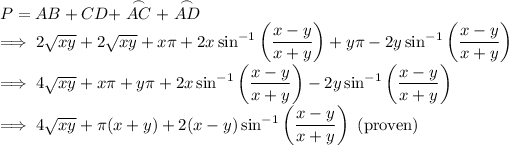See below
Explanation:
Refer to the attachment (i)
Observe that
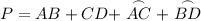
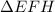 and
and
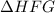 are right angle triangles as well as congruent
are right angle triangles as well as congruent- Rectangle ABFE is congruent to Rectangle GFDC
Consider ∆EFH
- HF(hypotenuse)=x+y
- EH(opposite side)=x-y
So,
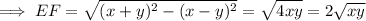 . . . . . using Pythagorean theorem.
. . . . . using Pythagorean theorem.
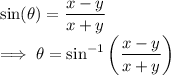
. . . . . using trigonometry
Now we can easily deduce that
Notice that
Recall that
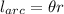
Therefore,
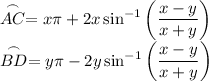
So,