Question

Find the midpoint of a segment with endpoints of 4 – 3i and –2 + 7i.

Answer 1

Midpoint is 1 + 2i

Explanation:

Given that endpoints are
`\displaystyle{4-3i}` and
`\displaystyle{-2+7i}`. The definition of complex number is that
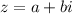`\displaystyle{z = a+bi}` where a is real part and b is imaginary part. In coordinate plane, the equation can be represented as a position vector with initial as origin point and final as (a,b).

So (a,b) in complex number represents the equation
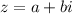`\displaystyle{z = a+bi}`. If we are given two complex equations:

`\displaystyle{z = a+bi}\\\displaystyle{w = c+di}`

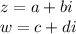
Then we can rewrite both as in:

`\displaystyle{z = (a,b)}\\\displaystyle{w = (c,d)}`

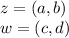
From the property:

`\displaystyle{(a,b) + (c,d) = (a+c, b+d)}`

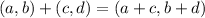
Since we are finding midpoint, we'd have to divide both components by 2. So our formula will be:

`\displaystyle{M_(z+w)= \left((a+c)/(2), (b+d)/(2)\right)}`

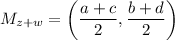
Determine that:

• 
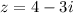  `\displaystyle{z=4-3i}` so a = 4 and b = -3
• 
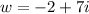  `\displaystyle{w = -2 + 7i}` so c = -2 and d = 7

Therefore:

`\displaystyle{M_(z+w)= \left((4+(-2))/(2), (-3+7)/(2)\right)}\\\\\displaystyle{M_(z+w)= \left((4-2)/(2), (4)/(2)\right)}\\\\\displaystyle{M_(z+w)= \left((2)/(2), 2\right)}\\\\\displaystyle{M_(z+w)= \left(1,2\right)}`

So our midpoint will be at (1,2) which then can be rewritten back to 1 + 2i through position vector.