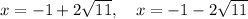Question

Solve the equation x² + 2x=43 Give your answer to 1 decimal place.

Found from Collins Maths Ks3 Higher Level​

Answer 1

Answer: It would need ten correct answers and one incorrect answer, ... 1 a an odd number (multiply the position in the sequence by 2 then subtract 1).

Explanation:

Answer 2

`x=-1+2√(11), \quad x=-1-2√(11)`

Explanation:

Given equation:

`x^2+2x=43`

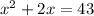
Solve by the method of Completing the Square.

Step 1:

When completing the square for an equation in the form ax² + bx + c = 0, the first step is to move the constant to the right side of the equation.

This has already been done in the given equation:

`x^2+2x=43`

Step 2:

Add the square of half the coefficient of x to both sides. This forms a perfect square trinomial on the left side:

`\implies x^2+2x+\left((2)/(2)\right)^2=43+\left((2)/(2)\right)^2`

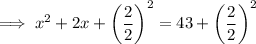
Simplify:

`\implies x^2+2x+\left(1\right)^2=43+\left(1\right)^2`

`\implies x^2+2x+1=43+1`

`\implies x^2+2x+1=44`

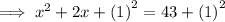
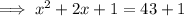
Step 3:

Factor the perfect square trinomial on the left side to complete the square:

`\implies (x+1)^2=44`

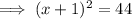
Step 4:

To solve, square root both sides:

`\implies √((x+1)^2)=√(44)`

`\implies x+1=\pm√(4 \cdot 11)`

`\implies x+1=\pm√(4)√(11)`

`\implies x+1=\pm2√(11)`

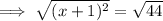
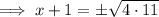
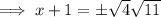
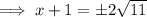
Subtract 1 from both sides:

`\implies x+1-1=-1\pm2√(11)`

`\implies x=-1\pm2√(11)`

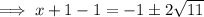
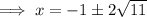
Solution:

Therefore, the solutions of the given equation are:

`x=-1+2√(11), \quad x=-1-2√(11)`