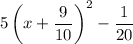Question

Write in the form p(x +q)² + r...
5x² + 9x +4​

Answer 1

`2(7x+`
`2)^(2)`

Explanation:

5x+9x= 14x

14x+4= 2(7x+2)²

2(7x+2)²= 196x+16

Answer 2

`5\left(x+(9)/(10)\right)^2-(1)/(20)`

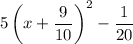
Explanation:

Given:

`5x^2+9x+4`

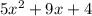
Factor out the coefficient of the leading term from the first two terms:

`\implies 5\left(x^2+(9)/(5)x\right)+4`

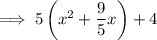
Add the square of half the coefficient of the x term inside the parentheses and subtract its distributed value from the expression:

`\implies 5\left(x^2+(9)/(5)x+\left(\frac{(9)/(5)}2\right)^2\right)+4-5\left(\frac{(9)/(5)}2\right)^2`

Simplify:

`\implies 5\left(x^2+(9)/(5)x+\left((9)/(10)\right)^2\right)+4-5\left((9)/(10)\right)^2`

`\implies 5\left(x^2+(9)/(5)x+(81)/(100)\right)+4-5\left((81)/(100)\right)`

`\implies 5\left(x^2+(9)/(5)x+(81)/(100)\right)+4-(405)/(100)`

`\implies 5\left(x^2+(9)/(5)x+(81)/(100)\right)-(1)/(20)`

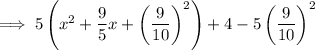
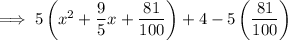
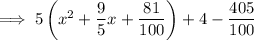
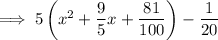
Factor the perfect trinomial contained within the parentheses:

`\implies 5\left(x+(9)/(10)\right)^2-(1)/(20)`

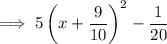
Therefore, the given expression written in vertex form is:

`5\left(x+(9)/(10)\right)^2-(1)/(20)`