Answer:
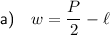
b) w = 65 yd
c) 4.83% (2 d.p.)
Explanation:
Perimeter formula
where:
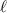 is the length
is the length
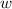 is the width
is the width
Part (a)
To solve the formula for w, use arithmetic operations to isolate w:
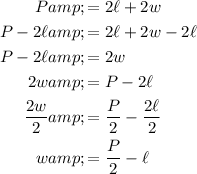
Part (b)
Given:
Substitute the given values into the formula for width found in part (a) to find w:
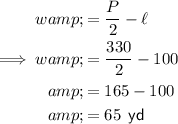
Part (c)
Area of a rectangle
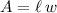
where:
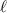 is the length
is the length
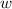 is the width
is the width
Therefore, the area of the field is:

Area of a circle
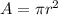
where:
 is the radius
is the radius
Therefore, the area of the central circle of the field is:

To find the percent of the field that is inside the circle, divide the found area of the circle by the found area of the field, and multiply by 100:
