Answer:
50
Explanation:
Given:
- Volume of the Moon = 2.0 × 10¹⁰ km³
- Volume of the Earth = 1.0 × 10¹² km³
To find how many Moon volumes could fit inside of the volume of the Earth, divide the given volume of the Earth by the given volume of the Moon:
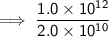
Separate:
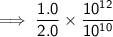

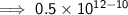
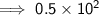
Simplify:
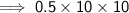
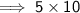
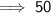
Therefore, 50 Moon volumes could fit inside the volume of the Earth.