Answer:
EF = 5 units
GH = 6.4 units (nearest tenth)
Explanation:
Given:
To find the length of EF, use the distance formula.
Distance between two points
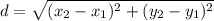
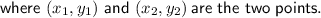
Substitute the given points into the formula:
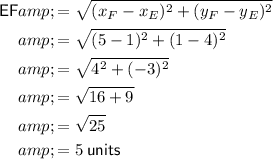
Therefore, the length of EF is 5 units.
--------------------------------------------------------------------------------------------------
Given:
To find the length of GH, use the distance formula.
Distance between two points
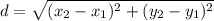
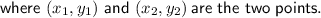
Substitute the given points into the formula:
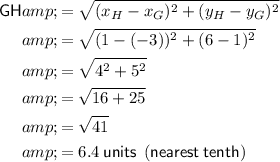
Therefore, the length of GH is about 6.4 units (nearest tenth).