Question

How many liters of water should be added to 18 liters of a 14% bleach solution SO that the resulting solution contains

only 10% bleach?
Original (L)
Added (L)
New (L)
Amount of Bleach
2.52
0
Amount of Solution
18
X
O 1.8 liters
O 7.2 liters
• 15.5 liters
• 25.2 liters

Answer 1

B) 7.2 liters

Explanation:

To determine how many liters of water should be added to 18 liters of a 14% bleach solution so that the resulting solution contains only 10% bleach, first calculate the amount of bleach in the original volume of the solution:

`\begin{aligned} \sf Bleach&=14\%\;\textsf{of}\;18\; \sf liters \\&= 0.14 * 18 \\&= 2.52\; \sf liters\end{aligned}`

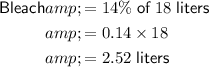
Therefore, there is 2.52 liters of bleach in the original volume of the solution.

If the amount of bleach in the solution should be 10%, then the new volume of the solution should be:

`\begin{aligned}10\%&=2.52\; \sf liters\\10\% * 10&= 2.52\; \textsf{liters} * 10\\100\%& = 25.2\; \sf liters\end{aligned}`

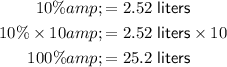
To find the amount of water that should be added to the original volume of the solution, subtract the original volume of the solution from the new volume of the solution:

`\begin{aligned} \textsf{Water}&=\textsf{New volume}-\textsf{Original volume}\\&=25.2\; \textsf{liters} - 18\; \textsf{liters}\\&= 7.2\; \sf liters\end{aligned}`

Therefore, 7.2 liters of water should be added to 18 liters of a 14% bleach solution so that the resulting solution contains only 10% bleach.