Answer:
-60 m/s²
Explanation:
We are not given the velocity of the plane at landing but we are given velocities at two time periods
V₅, the velocity of the plane 5 seconds after landing is 110 m/s
Plugging this into the velocity equation we get
 (1)
(1)
Similarly
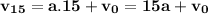 (2)
(2)
Subtract (1) from
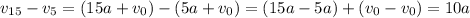
Therefore
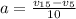
Given

this evaluates to
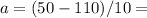 -60 m/s²
-60 m/s²
The negative value is because the plane is actually decelerating which is a negative number