I'm assuming you mean
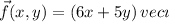
It's a bit odd that there is no
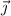 -component, but at any rate we want to find a scalar function
-component, but at any rate we want to find a scalar function
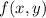 for which
for which
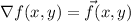
This would mean
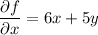
and
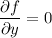
The second equation tells us
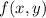 is a function that only depends on
is a function that only depends on
 . But the first equation tells us
. But the first equation tells us
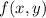 is a function of both
is a function of both
 and
and
 . No such function exists, so the given field is not conservative.
. No such function exists, so the given field is not conservative.