Answer:
B.
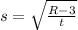
Explanation:
Solve for s in the equation:
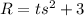
Make s the subject of formula by collecting like terms.
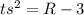
Divide both sides by the coefficient of s²
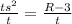

Square root both sides because s is squared.
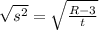
Therefore:
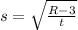 is the final answer.
is the final answer.
Option A is almost correct but the square root is not for only
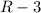 but for
but for
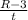
I hope this helps