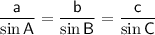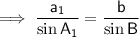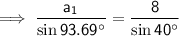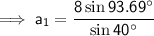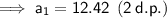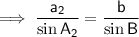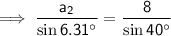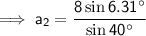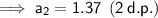Answer:
Two triangles are produced.
C₁ ≈ 46.31° (2 d.p.)
A₁ ≈ 93.69° (2 d.p.)
a₁ ≈ 12.42 (2 d.p.)
C₂ ≈ 133.69° (2 d.p.)
A₂ ≈ 6.31° (2 d.p.)
a₂ ≈ 1.37 (2 d.p.)
Explanation:
Given:
Two triangles can be produced with the given information (see attached).
Angle C can be acute (less than 90°) and obtuse (greater than 90° and less than 180°).
Use the Sine Rule to find the measure of angle C.
Sine Rule
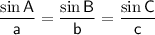
(where A, B and C are the angles and a, b and c are the sides opposite the angles).
Substitute the given information into the Sine Rule formula and solve for C:
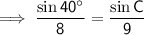
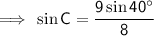
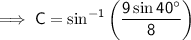
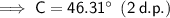
The found angle is acute and is therefore the measure of angle C₁.
If C₁ is acute, then its supplement is obtuse as sin θ = sin (180° - θ), where 90° < θ < 180°.
Therefore, angle C₂ is:
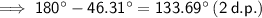
Therefore:
- C₁ ≈ 46.31° (2 d.p.)
- C₂ ≈ 133.69° (2 d.p.)
Now we have found angles C₁ and C₂, use the theorem of interior angles of a triangle sum to 180° to find A₁ and A₂.
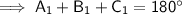
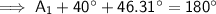
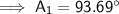
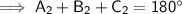
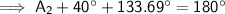
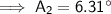
Finally, use the Sine Rule again to find the measure of side a for each triangle.