Question

Solve for work when

Force is 1.41 x 10^4 N
Distance 84.9 m
Angle 45°

Show work

Answer 1

So, the value of the work is approximately 84.65 J.

Introduction

Hi ! Here I will help you to discuss the subject about work that caused by force in amount value of angle. Work is affected by the force and displacement.

• If related to the magnitude of the force, the amount of work will be proportional to the magnitude of the applied force. Thats mean, if the value of the force that applied on it is greater, then the value of the work will be greater.
• If related to the magnitude of shift, the amount of work will be proportional to the magnitude of shift of object. Thats mean, if the value of the shift on it is greater, then the value of the work will be greater.

Formula Used

The work done by a moving object can be expressed in the equation:

If the Angle Is Ignored

`\boxed{\sf{\bold{W = F * s}}}`

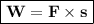
If the Angle Effect on Work

`\boxed{\sf{\bold{W = F * s * \cos(\theta)}}}`

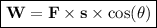
With the following condition:

• W = work that done by object (J)
• F = force that applied (N)
• s = shift or distance (m)
• 
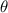  `\sf{\theta}` = angle of elevation (°)

Solution

We know that :

• F = force that applied =
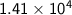  `\sf{1.41 * 10^4}` N
• s = shift or distance = 84.9 m
• 
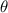  `\sf{\theta}` = angle of elevation = 45°

What was asked ?

• W = work that done by object = ... J

Step by step :

`\sf{W = F * s * \cos(\theta)}`

`\sf{W = (1.41 \cdot 10^4) * 84.9 * \cos(45^o)}`

`\sf{W = (1.41 \cdot 10^4) * 84.9 * (√(2))/(2)}`

`\sf{W = 119.709 * (√(2))/(2)}`

`\sf{W = 59.8545 √(2)}`

`\boxed{\sf{W \approx 84.65 \: J}}`

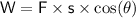
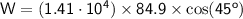
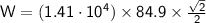
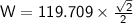
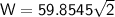
Conclusion

So, the value of the work is approximately 84.65 J.