Answer:
a) (i) 86.614 in
(ii) 47.6377 in
(iii) 1.584 m
b) width = 1.107 m (3 d.p.)
c) D = 1.135 m (3 d.p.)
Explanation:
Part (a)
Question (i)
Given:

Question (ii)
Substitute the found value of D from part (i) into the given formula for D and solve for S:
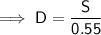
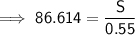
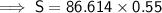
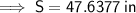
Question (iii)
Given:
Substitute the given values into the given formula for M and solve for M:
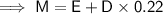
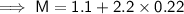
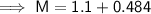
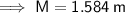
Part (b)
Given:
- S = 50 in
- Ratio of width to height = 16 : 9
Pythagoras Theorem

where:
- a and b are the legs of the right triangle.
- c is the hypotenuse (longest side) of the right triangle.
Use Pythagoras Theorem to find the ratio of the diagonal S to the width and height:

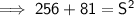
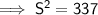
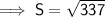
Therefore, the ratio of width to height to diagonal S of the TV is:
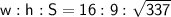
If S = 50 in then:
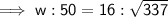

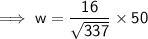
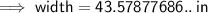
To convert to meters, divide the width in inches by 39.37:
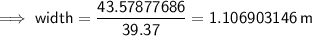
Therefore, the width of the TV is 1.107 m (3 d.p.).
Part (c)
If the TV is mounted in the position from part (aiii), where the midpoint of the TV is 1.584 m from the ground, and the height of the TV is 62.2cm, then:
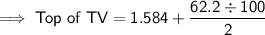

Therefore, the top of the TV from the floor is 1.895m.
As E = 1.1 m, the vertical distance between the eye level and the top of the TV is:
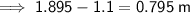
To find D, model as a right triangle (see attached) and use the tan trigonometric ratio to find the shortest value of D.
Tan trigonometric ratio
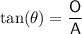
where:
 is the angle
is the angle- O is the side opposite the angle
- A is the side adjacent the angle
Given:
 = 35°
= 35°- O = 0.795 m
- A = D m
Substitute the values into the formula and solve for D:

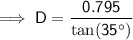
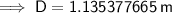
Therefore, the shortest distance that the sofa should be placed from the wall is 1.135 m (3 d.p.).