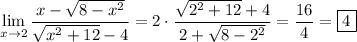Question

How do i solve this question?​

Answer 1

The function itself is not well-defined at
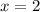`x=2` because both numerator and denominator are equal to zero there, so it's discontinuous there. We attempt to remove this discontinuity.

Rationalize the numerator and denominator.

`\displaystyle (x - √(8 - x^2))/(√(x^2 + 12) - 4) \cdot (x + √(8 - x^2))/(x + √(8 - x^2)) \cdot (√(x^2+12) + 4)/(√(x^2 + 12) + 4)`

`\displaystyle = (x^2 - \left(√(8-x^2)\right)^2)/(\left(√(x^2+12)\right)^2 - 4^2) \cdot (√(x^2 + 12) + 4)/(x + √(8 - x^2))`

`\displaystyle = (x^2 - (8-x^2))/((x^2+12)-16) \cdot (√(x^2 + 12) + 4)/(x + √(8 - x^2))`

`\displaystyle = (2x^2 - 8)/(x^2 - 4) \cdot (√(x^2 + 12) + 4)/(x + √(8 - x^2))`

`\displaystyle = 2 ((x-2)(x+2))/((x-2)(x+4)) \cdot (√(x^2 + 12) + 4)/(x + √(8 - x^2))`

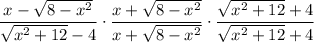
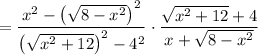
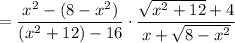
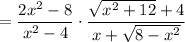
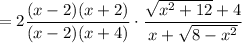
Then in the limit, since
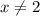`x\\eq2`, we can cancel both factors of
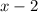`x-2` and
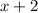`x+2`, subsequently removing the discontinuities at
`x=\pm2`, and we're left with

`\displaystyle \lim_(x\to2) (x-√(8-x^2))/(√(x^2+12)-4) = 2 \lim_(x\to2) (√(x^2+12)+4)/(x+√(8-x^2))`

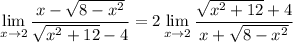
which is now continuous at
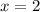`x=2`, so we can evaluate directly.

`\displaystyle \lim_(x\to2) (x-√(8-x^2))/(√(x^2+12)-4) = 2 \cdot (√(2^2+12)+4)/(2+√(8-2^2)) = \frac{16}4 = \boxed{4}`