Answer:
Coordinates of M and N are
(-3, -2.5) and (3, -1)
The order is not important since we are not told where M and N points actually are. The attached graph will make this clear
Explanation:
The two equations are
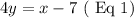
and
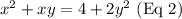
Adding 7 to both sides of Eq 1 gives us
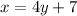
Eq2 can be re-written as
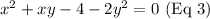
The above is done by subtracting
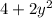 on both sides of Eq 2
on both sides of Eq 2
Substituting for
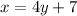 in Eq 3 gives us
in Eq 3 gives us
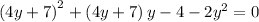
Let's examine the first two terms and simplify
 =
=
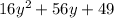 (A)
(A)
 (B)
(B)
So Eq 3 can be reduced to a quadratic equation with one variable,

(A) + (B) -
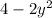 =
=
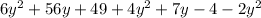
Grouping like terms we get

Adding similar terms we get
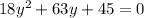
We can divide both sides of the equation by 9 to make it easier to solve using the equation for the solutions of a quadratic equation
Dividing both sides by 9 we get

Use the quadratic formula
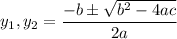
where a is the coefficient of
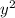 ,
,
 the coefficient of
the coefficient of
 and
and
 the constant
the constant
Here
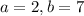 and
and
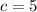
So we get
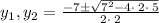 =
=
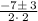
The above is obtained by noting that
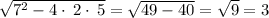
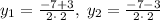
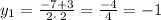 (using the + component)
(using the + component)
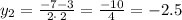
Find
 and
and
 by substituting each of these values in the equation for
by substituting each of these values in the equation for

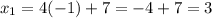
Therefore the coordinates of M and N are
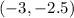 and
and

The order is not important since we are not told which are M and N points. See the attached graph for a visual depiction
Hope that helps :)