Answer:
Domain:
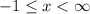 or in interval notation
or in interval notation
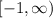
Range:
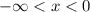 or, in interval notation
or, in interval notation

And yes, you can graph it but not necessary for a problem like this. I have provided the graph
Explanation:
This is known as a piecewise function. Two different expressions for two different intervals
The domain of a function f(x) is the range of input values for which f(x) is real and defined
For example, the function
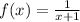 is the set of all x values except for x = -1. Because at x = -1, the denominator will be 0 and division by 0 does not result in a real value for f(x). (It is actually defined as
is the set of all x values except for x = -1. Because at x = -1, the denominator will be 0 and division by 0 does not result in a real value for f(x). (It is actually defined as
 )
)
For
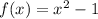 , the domain is
, the domain is
 since either negative x or positive x will result in a real value for the function but not at
since either negative x or positive x will result in a real value for the function but not at
 or
or
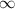
But the above function is only defined for
 . So if we consider this part of the function the domain is
. So if we consider this part of the function the domain is

expressed in interval notation: [-1, 1]
The range is max-min.
At x = 0, min = -1, at x = ∞, max = ∞
So range of this part of the piecewise function is [-1, ∞)
For the second interval f(x) =
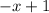 at
at
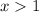 . Since x can range from > 1 to
. Since x can range from > 1 to
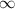 , the function is valid only for 1 <x <
, the function is valid only for 1 <x <
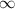
So the domain of this part of the function is
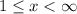 expressed in interval notation as
expressed in interval notation as
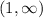
For range,
At x = 1 , the function value is -1 + 1 = 0 (max)
At x =
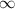 , the function value is
, the function value is
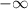 (min)
(min)
So range of this part of the function is (-∞, 0)
Taking both into consideration, we choose the most appropriate lowest and highest levels. This is called the union of the two domains.
Hence the domain for the entire piecewise function is
[-1, ∞)
Range of the entire piecewise function is
(-∞, 0)
(I had to do a lot of typing here. Not sure if I made typos. Please check)