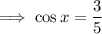Question

I'm confused! TRIGONOMETRY​

Answer 1

Sin of angle is equal to the opposite side(4) over the hypotenuse(5) of the triangle so you have two sides to a triangle 4&5 now use Pythagorean theorem to find other side 5^2=4^2 + x^2 you end up with x=3 which is your adjacent side of the triangle to the angle x now cos(x) is adjacent over hypotenuse so cos(x)=3/5

Answer 2

`\cos x=(3)/(5)`

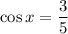
Explanation:

As angle x is less that 90°, we can model this as a right triangle and use Pythagoras Theorem and trigonometric ratios to find cos(x).

Trigonometric ratios

`\sf \sin(\theta)=(O)/(H)\quad\cos(\theta)=(A)/(H)\quad\tan(\theta)=(O)/(A)`

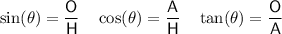
where:

• 
  `\theta` is the angle.
• O is the side opposite the angle.
• A is the side adjacent the angle.
• H is the hypotenuse (the side opposite the right angle).

Given:

• sin(x) = ⁴/₅

Compare with the sine trigonometric ratio:

• O = 4
• H = 5

Pythagoras Theorem

`a^2+b^2=c^2`

(where a and b are the legs, and c is the hypotenuse, of a right triangle)

Use Pythagoras Theorem to find the missing side of the right triangle:

`\implies 4^2+b^2=5^2`

`\implies 16+b^2=25`

`\implies b^2=25-16`

`\implies b^2=9`

`\implies b=√(9)`

`\implies b=3`

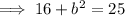
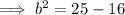
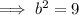
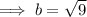
The missing side is the side adjacent to angle x in a right triangle.

Therefore, to find cos(x):

• A = 3 units
• H = 5 units

Substitute these values into the cos trigonometric ratio:

`\implies \cos x=(3)/(5)`