Question

Pls help! TRIGONOMETRY​

Answer 1

x = 150 degree

x = 210 degree

Explanation:

cos(x) = -cos(30) = -√3/2

x = 150 degree

x = 210 degree

Answer 2

θ = 150°, 210°

Explanation:

Given:

`\cos \theta=- \cos 30^(\circ), \quad 0 < \theta < 360^(\circ)`

We know from trigonometric values of special angles that :

`\cos 30^(\circ)=(√(3))/(2)`

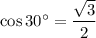
and that 30° is in Quadrant I.

Therefore:

`-\cos 30^(\circ)=-(√(3))/(2)`

`\begin{array} c\cline{1-2} \sf Quadrant & \sf Reference \: Angle\\\cline{1-2} \rm I & \theta\\\cline{1-2} \rm II & 180^(\circ)-\theta \\\cline{1-2} \rm III & \theta - 180^(\circ) \\\cline{1-2} \rm IV & 360^(\circ) - \theta \\\cline{1-2} \end{array}`

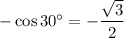
Cosine is negative In Quadrants II and III. Therefore, use the above table to find the reference angles of 30° that make the cosine of the angle negative:

`\cos (180-30)^(\circ)=-(√(3))/(2) \implies \cos 150^(\circ)=-(√(3))/(2)`

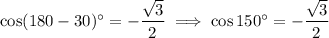
and:

`\cos (30-180)^(\circ)=-(√(3))/(2) \implies \cos (-150^(\circ))=-(√(3))/(2)`

Therefore, θ = 150° ± 360°n, -150° ± 360°n.

So the measure of θ in the given interval is 150° and 210°.