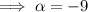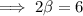Answer:
-9, 3 and 6
Explanation:
Given cubic polynomial equation:
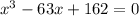
- Let α = first zero
- Let β = second zero
- Let 2β = third zero (since one zero is double another zero).

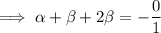
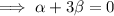
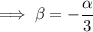


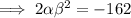
Substitute the found expression for β into the product equation:
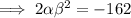
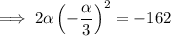
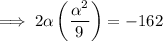
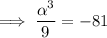
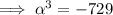
![\implies \alpha=\sqrt[3]{-729}](https://img.qammunity.org/2023/formulas/mathematics/college/7ihnkpsfp60dep2ayplk33akux302sll37.png)
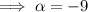
Substitute the found value of α into the expression for β :
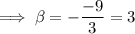
Therefore, the zeros are: