Question

18. Given f(x) = √(x + 1) and g(x) = 4^x what is the domain of (f + g)(x)?

a) (xER)
B)(XER/X<=-1)
C) (XER/X=>-1)
D)(XER/X<-1)
E)(XER/X>-1)

Answer 1

`x \ge-1`

Explanation:

So you have the following equations:

`f(x)=√(x+1)`

`g(x)=4^x`

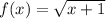
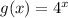
Adding the two together, we get:
`(f+g)(x)=√(x+1)+4^x`

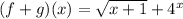
There's nothing here that's really changing the domain of:
`f(x)`, which has a domain of:
`x\ge-1` since when x is any less than -1, x+1 will evaluate to a negative value, and the square root of a negative number has no real solution.

The domain of an exponential, specifically when the base is positive, has no domain restrictions. In other words it's defined for all values of x.

So the domain will be dependent on the domain of f(x), which is only defined for values greater than or equal to -1