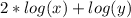Question

HELLOOOO HELP PLEASE

Answer 1

`2*log(x)+log(y)`

Explanation:

So, there are two logarithmic identities you're going to need to know.

Logarithm of a power:

`log_ba^c=c*log_ba`

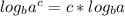
So to provide a quick proof and intuition as to why this works, let's consider the following logarithm:
`log_ba=x\implies b^x=a`

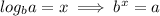
Now if we raise both sides to the power of c, we get the following equation:
`(b^x)^c=a^c`

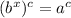
Using the exponential identity:
`(x^a)^c=x^(a*c)`

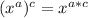
We get the equation:
`b^(xc)=a^c`

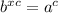
If we convert this back into logarithmic form we get:
`log_ba^c=x*c`

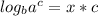
Since x was the basic logarithm we started with, we substitute it back in, to get the equation:
`log_ba^c=c*log_ba`

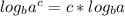
Now the second logarithmic property you need to know is

The Logarithm of a Product:

`log_b{ac}=log_ba+log_bc`

Now for a quick proof, let's just say:
`x=log_ba\text{ and }y=log_bc`

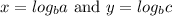
Now rewriting them both in exponential form, we get the equations:

`b^x=a\\b^y=c`

We can multiply a * c, and since b^x = a, and b^y = c, we can substitute that in for a * c, to get the following equation:

`b^x*b^y=a*c`

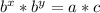
Using the exponential identity:
`x^(a)*x^b=x^(a+b)`, we can rewrite the equation as:

`b^(x+y)=ac`

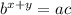
taking the logarithm of both sides, we get:

`log_bac=x+y`

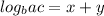
Since x and y are just the logarithms we started with, we can substitute them back in to get:
`log_bac=log_ba+log_bc`

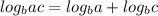
Now let's use these identities to rewrite the equation you gave

`log(x^2y)`

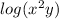
As you can see, this is a log of products, so we can separate it into two logarithms (with the same base)

`log(x^2)+log(y)`

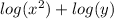
Now using the logarithm of a power to rewrite the log(x^2) we get:

`2*log(x)+log(y)`