Question

If f(1) = 6 and f(n) = 4f (n-1) then find the value of f (5) (please help im stuck)

Answer 1

Answer: 1536

===================================================

Work Shown:

Replace n with 2

f(n) = 4*f(n-1)

f(2) = 4*f(2-1)

f(2) = 4*f(1)

f(2) = 4*6 ................. replace f(1) with 6; since f(1) = 6

f(2) = 24

Repeat for n = 3

f(n) = 4*f(n-1)

f(3) = 4*f(3-1)

f(3) = 4*f(2)

f(3) = 4*24 ................. replace f(2) with 24; since f(2) = 24

f(3) = 96

Plug in n = 4

f(n) = 4*f(n-1)

f(4) = 4*f(4-1)

f(4) = 4*f(3)

f(4) = 4*96 ................. replace f(3) with 96; since f(3) = 96

f(4) = 384

And finally n = 5

f(n) = 4*f(n-1)

f(5) = 4*f(5-1)

f(5) = 4*f(4)

f(5) = 4*384 ................. replace f(4) with 384; since f(4) = 384

f(5) = 1536 which is the final answer

The sequence is: 6, 24, 96, 384, 1536, ....

As you can see, each new term of the recursive sequence is built off the previous one.

Each time we need a new term, we multiply by 4.

The closed form equation is
`a_n = 6*4^(n-1)`

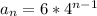
If you plugged in n = 5, then
`a_5 = 6*4^(5-1) = \boldsymbol{1536}`

For more information, search out geometric sequences.