Answer:
The sum of the first 8 terms is 39360
Explanation:
A geometric series is a series of numbers that have a common ratio. The series given to us is the following: 12, 36, 108,... We can see that there is a common ratio of 3 (108/36 = 36/12 = 3). Therefore, this series is a geometric series. Since we know that, we can use the sum of geometric series formula to find the sum of the first 8 terms:
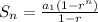
In this formula,
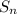 is the sum of the first n terms of the series (in our case, n would be 8).
is the sum of the first n terms of the series (in our case, n would be 8).
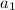 is the first term in the series, which is 12 in our case. r is the common ratio between the terms (which is 3). Finally, n is the number of terms, and since we know we are looking for the sum of the first 8 terms, n is 8. Now, we can plug in our known quantities and solve:
is the first term in the series, which is 12 in our case. r is the common ratio between the terms (which is 3). Finally, n is the number of terms, and since we know we are looking for the sum of the first 8 terms, n is 8. Now, we can plug in our known quantities and solve:
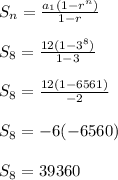
Therefore, the sum of the first 8 terms is 39360