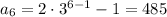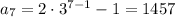Let
 denote the
denote the
 -th term in the sequence. By checking the forward differences, we observe
-th term in the sequence. By checking the forward differences, we observe
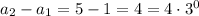
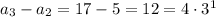
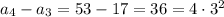
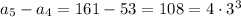
The pattern is

So we find
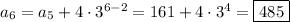
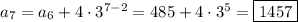
We also could have solved for
 first. By substitution,
first. By substitution,
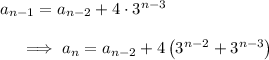
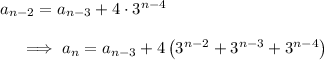
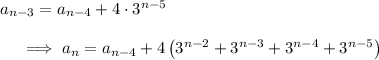
and so on. After so many iterations of this, we see the pattern
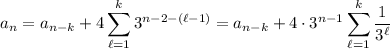
so that for
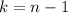 , we get
, we get
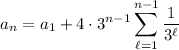
Let
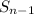 be the remaining sum. We have
be the remaining sum. We have

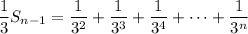

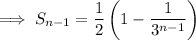
and so
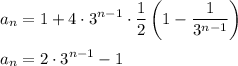
Then