Question

What are the restrictions on the domain of g°h?

X> _____

Answer 1

Answer: x ≥ 6

Explanation:

The notation shown in your question means "g of h of x"

So we are taking whatever output we get from function 'h' and then applying function 'g' to that output.

For example, suppose I have two functions, 'a' and 'b'. Further suppose a(x) = 2x and b(x) = x +5

If I want a°b, that is really a[b(x)] = a(x + 5) = 2(x+5) = 2x + 10

In your case, we want g[h(x)] = g(2x-8) =
`√((2x - 8) - 4)` =
`√(2x - 12)`

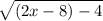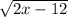
Now, we know that in the set of Real numbers, we cannot take a square root of a negative number.

Therefore, (2x - 12) must be zero or greater.

So, our restriction is that 2x - 12 ≥ 0. But of course we must simplify.

Add 12 to both sides ---> 2x ≥ 12

Divide both sides by 2 ---> x ≥ 6

That is the restriction for (g ° h)(x) ---> x ≥ 6

Hope this helps!

Answer 2

Answer:x=6

Step-by-step explanation:g o h is a composition function

First we find g o h

g o h is g(h(x))

We plug in h(x) in g(x)

We replace x with 2x-8 in g(x)

To find domain we look at the domain of h(x) first

Domain of h(x) is set of all real numbers

now we look at the domain of g(h(x))

Negative number inside the square root is imaginary. so we ignore negative number inside the square root

So to find domain we set 2x - 12 >=0 and solve for x

2x - 12 >=0

add both sides by 12

2x >= 12

divide both sides by 2

x > = 6