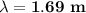Question

A wave has an amplitude of 0.0800 m and is moving 7.33 m/s. One oscillator in the wave takes 0.115 s to go from the lowest point in its motion to the highest point. Find the wavelength of the wave.

(Unit = m)

Answer 1

1.69 m

Step-by-step explanation:

To solve this problem, we can use the universal wave equation:

`\boxed{v = (\lambda)/(T)}`,

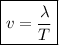where:

v = wave speed

λ = wavelength

T = time period

In the question, we are told that an oscillator in the wave takes 0.115 s to go from the the lowest point in its motion to the highest point, but we know that the time period of an oscillation is the time taken for the oscillator to return to the position it was in at the beginning of the oscillation. Therefore the time period can be the time taken for the oscillator to start at the highest point and then return to the highest point after one complete oscillation.

This means that the time period is actually double of 0.115 s:

`T = 0.115 * 2`

=
`\bf 0.23 \space\ s`

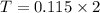
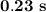
Now we can simply substitute the values into the wave equation:

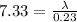
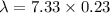
`7.33 = (\lambda)/(0.23)`

⇒
`\lambda = 7.33 * 0.23`

⇒
`\lambda = \bf 1.69 \space\ m`