Answer:
30
Explanation:
Distance Formula
In a 2 dimensional plane, the distance between points (x1, y1) and (x2, y2) is given by the Pythagorean theorem:
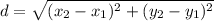
Here we have (x1, y1) = (-13, 16) and (x2, y2) = (5,-8)
Simply substitute these values into the above equation to get the result
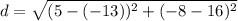
=
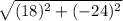
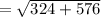
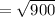
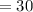 (Answer)
(Answer)