(3x^(8)*7x^(3) )/(3x^(6)*7 ) can be written in the form 3a⋅7b where: a= and b=

Question

`(3x^(8)*7x^(3) )/(3x^(6)*7 )` can be written in the form 3a⋅7b where: a= and b=

Answer 1

`a = (x^2)/(3) \quad \textsf{and} \quad b = (x^3)/(7)`

Explanation:

Given expression:

`(3x^(8) \cdot 7x^(3) )/(3x^(6) \cdot 7 )`

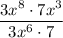
There are several ways this problem can be approached, and therefore many different answers. The goal is to reduce the given expression to a simple product of two terms in x, set that to the given form 3a⋅7b then solve for a and b.

`\implies (3x^(8) \cdot 7x^(3) )/(3x^(6) \cdot 7)`

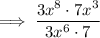
Cancel the common factors 3 and 7:

`\implies (\diagup\!\!\!\!3x^(8) \cdot \diagup\!\!\!\!7x^(3) )/(\diagup\!\!\!\!3x^(6) \cdot \diagup\!\!\!\!7)`

`\implies (x^8 \cdot x^3)/(x^6)`

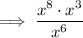
Separate the fraction:

`\implies (x^8)/(x^6) \cdot x^3`

`\textsf{Apply the quotient rule of exponents} \quad (a^b)/(a^c)=a^(b-c):`

`\implies x^(8-6) \cdot x^3`

`\implies x^(2) \cdot x^3`

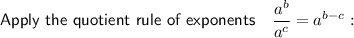
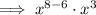
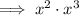
Now equate the simplified expression to the given form:

`\implies x^(2) \cdot x^3=3a \cdot 7b`

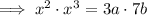
Therefore:

`\begin{aligned}x^(2) &=3a \:\: &\textsf{ and }\:\: \quad x^3 &=7b\\ \Rightarrow a & = (x^2)/(3) & \Rightarrow b & = (x^3)/(7)\end{aligned}`

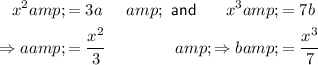
However, we could also separate them as:

`\begin{aligned}x^(3) &=3a \:\: &\textsf{ and }\:\: \quad x^2 &=7b\\ \Rightarrow a & = (x^3)/(3) & \Rightarrow b & = (x^2)/(7)\end{aligned}`

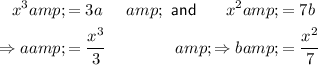
Another way of writing them would be to go back a few steps and separate the fraction in x terms differently:

`\implies (x^8 \cdot x^3)/(x^6)=x^8 \cdot (x^3)/(x^6)=x^8 \cdot x^(-3)`

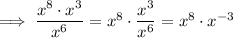
Therefore, this would give us:

`\begin{aligned}x^(8) &=3a \:\: &\textsf{ and }\:\: \quad x^(-3) &=7b\\ \Rightarrow a & = (x^8)/(3) & \Rightarrow b & = (1)/(7x^3)\end{aligned}`

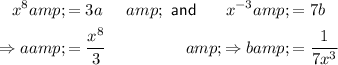
As the given expression reduces to x⁵, we can separate the x term in any way we like, so long as the coefficient of a is ¹/₃ and the coefficient of b is ¹/₇. Therefore, there are many possible answers.

Answer 2

`a=(x^2)/(3) \\\\ b= (x^3)/(7)`.

Explanation:

1. Write the expression.

`(3x^8*7x^3)/(3x^6*7)`

2. Separate into 2 fractions.

`(3x^8)/(3x^6) *(7x^3)/(7)`

3. Divide the left hand side fraction by 3 and the right one by 7.

`(3x^8)/(3x^6*(3)) *(7x^3)/(7(7))\\ \\(3x^8)/(9x^6) *(7x^3)/(49)`

4. Simplify.

`(x^2)/(3) *(x^3)/(7)`

5. Identify "a" and "b".

`a=(x^2)/(3) \\\\ b= (x^3)/(7)`

6. Rewrite in the form 3a⋅7b.

`3((x^2)/(3))*7((x^3)/(7))`

7. Verify.

If the re-writting was done correctly, then if we substitute x by a value both in the original expression and the re-written expression, it should give the same result. Let's test it with x= 2:

`(3(2)^8*7(2)^3)/(3(2)^6*7)=32\\\\3(((2)^2)/(3))*7(((2)^3)/(7))=32.`

8. Express your results.

`(3x^8)/(3x^6) *(7x^3)/(7)=3((x^2)/(3))*7((x^3)/(7))\\ \\a=(x^2)/(3) \\\\ b= (x^3)/(7)`