So, the particle's initial velocity was 7.453 m/s.
Introduction
Hi ! Here, I will help you to explain about the relationship between acceleration with changes in velocity and time. To be able to make changes in speed, a certain time interval is needed. If the detected change in velocity is negative, then the object will experience a deceleration. However, if the speed change detected is positive, then the object will experience an acceleration. Here is the equation that applies:
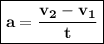
With the following condition :
- a = acceleration (m/s²)
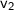 = final speed of the object (m/s)
= final speed of the object (m/s)
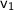 = initial speed of the object (m/s)
= initial speed of the object (m/s)- t = interval of the time (s)
Problem Solving
We know that :
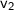 = final speed of the object = 9.31 m/s
= final speed of the object = 9.31 m/s- a = acceleration = 6.19 m/s²
- t = interval of the time = 0.300 s
What was asked :
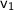 = initial speed of the object = ... m/s
= initial speed of the object = ... m/s
Step by step :

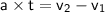
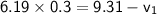
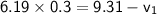
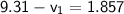
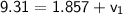
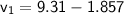

Conclusion
So, the particle's initial velocity was 7.453 m/s.