Question

Graph the line with the slope -4 and y-intercept -1

Answer 1

Answer: y=-4x-1

Explanation:

-1=-4(0)+b

-1=0+b

b=-1

y=-4x-1<==Graph this equation

Answer 2

See attachment.

Explanation:

Slope-intercept form of a linear equation:

`y=mx+b`

where:

• m is the slope.
• b is the y-intercept.

Given:

• slope = -4
• y-intercept = -1

Substitute the given values into the general formula to create an equation for the line:

`\implies y=-4x-1`

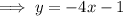
Graph the line

As the slope is negative, the line slopes downwards (as the x-value increases by 1, the y-value decreases by 4).

The y-intercept is the point at which the line crosses the y-axis, so when x = 0. Therefore, place a point at (0, -1).

Substitute any other value of x into the equation of the line to find another point on the line:

`x=2 \implies y=-4(2)-1=-9 \implies (2,-9)`

Plot point (2, -9).

Draw a straight line through both plotted points.