Question

A rectangular bedroom is 4 ft longer than it is wide. Its area is 252 ft2. What is the width of the room?

Answer 1

14 ft

Explanation:

Given:

• Bedroom is 4 ft longer than it is wide.
• Area is 252 ft².

Let x = width of the bedroom:

• width = x ft
• length = (x + 4) ft

Therefore:

`\begin{aligned}\textsf{Area of a rectangle} & = \sf width * length\\\implies 252 & = x(x+4)\\252 & = x^2+4x\\x^2+4x & = 252\end{aligned}`

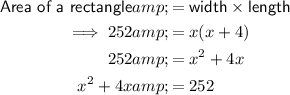
To find the value(s) of x, complete the square.

Add the square of half the coefficient of the term in x to both sides:

`\implies x^2+4x+\left((4)/(2)\right)^2=252+\left((4)/(2)\right)^2`

`\implies x^2+4x+4=256`

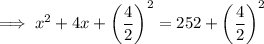
Factor the perfect trinomial on the left side:

`\implies (x+2)^2=256`

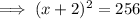
Square root both sides:

`\implies x+2= \pm √(256)`

`\implies x+2= \pm 16`

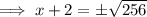
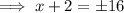
Therefore:

`\implies x=-2+16=14`

`\implies x=-2-16=-18`

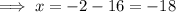
As width cannot be negative, the width of the room is 14 ft.