Question

|1/2b-8|=|1/4b-1|
b=____ and ____

Answer 1

b = 12 and 28

Explanation:

The absolute value equation |1/2b-8| = |1/4b-1| resolves to a piecewise linear function with three pieces. There are two solutions.

Domains

The absolute value function on the left has a turning point where its value is zero:

1/2b -8 = 0

b -16 = 0

b = 16

The absolute value function on the right has a turning point where its value is zero:

1/4b -1 = 0

b -4 = 0

b = 4

For b > 16, both absolute value functions are identity functions. In this domain, the equation is ...

1/2b -8 = 1/4b -1

For 4 < b < 16, the function on the left negates its argument, so the equation in this domain is ...

-(1/2b -8) = 1/4b -1

For b < 4, both functions negate their arguments, so the equation in this domain is ...

-(1/2b -8) = -(1/4b -1)

For the purpose of finding the value of b, this is effectively identical to the equation for b > 16. (The value of b does not change if we multiply both sides of the equation by -1.)

Solutions

Domain b < 4 ∪ 16 < b

1/2b -8 = 1/4b -1

2b -32 = b -4 . . . . . . . . multiply by 4

b = 28 . . . . . . . . . . . . add 32-b to both sides

This solution is in the domain of the equation, so is one of the solutions to the original equation.

Domain 4 < b < 16

-(1/2b -8) = 1/4b -1 . . . . equation in this domain

-2b +32 = b -4 . . . . . . multiply by 4

36 = 3b . . . . . . . . . . . add 2b+4 to both sides

12 = b . . . . . . . . . . . . divide by 3

This solution is in the domain of the equation, so is the other solution to the original equation.

Graph

For the purposes of the graph, we have define the function g(b) to be the difference of the two absolute value functions. The solutions are found where g(x) = 0, the x-intercepts. The graph shows those to be ...

b = 12 and b = 28

__

Additional comment

Defining g(b) = |1/2b-8| -|1/4b-1|, we can rewrite it as ...

`g(b)=\begin{cases}7-(1)/(4)b&\text{for }b < 4\\-(3)/(4)b+9&\text{for }4\le b < 16\\(1)/(4)b-7&\text{for }16\le b\end{cases}`

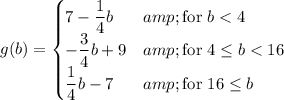
Then the solutions are the values of b that make g(b) = 0.