Question

PLEASE HELP I just need number 3

Answer 1

• L/T²
• m/s²

Explanation:

You want the dimensions and SI units of acceleration, given the dimensions of velocity and the relationship between velocity and acceleration.

Units of change in velocity

Dimensions can be treated algebraically as though they were variables. That is, some value together with its dimensions, will only be a "like term" with a value that has identical dimensions. Only like terms can be added or subtracted, and the sum or difference will have the same dimensions.

`v_1=a\frac{\text{L}}{\text{T}}\\\\v_2=b\frac{\text{L}}{\text{T}}\\\\\Delta v=v_2-v_1=b\frac{\text{L}}{\text{T}}-a\frac{\text{L}}{\text{T}}=(b-a)\frac{\text{L}}{\text{T}}`

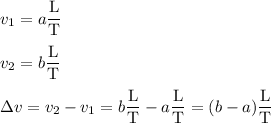
The dimensions of "change in velocity" are the same as those of velocity: length divided by time.

Units of acceleration

Acceleration is the change in velocity divided by the time in which it occurs. Its dimensions will be ...

`a=\frac{\left(\frac{\text{L}}{\text{T}}\right)}{\text{T}}=\boxed{\frac{\text{L}}{\text{T}^2}}\quad\text{dimensions of acceleration}`

SI units

The SI unit of length is the meter (m), and the SI unit of time is the second (s). This means the units of acceleration will be meters per second squared.

`\frac{\text{L}}{\text{T}^2}=\boxed{\frac{\text{m}}{\text{s}^2}=m\!\cdot\! s^(-2)}`

__

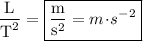
Additional comment

Take care not to confuse the product of meters and seconds (m·s) with the unit milliseconds (ms).

Ordinarily, an algebraic expression does not require a multiplication symbol between factors. However, it is wise to use available punctuation to make sure the expression is properly interpreted.