Question

Find the equation of the line that contains the points (5,4) and (6,7). Write the equation in the form y=mx+b and identify m and b.

m =?
b =?

Answer 1

Answer: y = 3x-11

m = 3

b = -11

=======================================================

Step-by-step explanation:

Let's find the slope

`(x_1,y_1) = (5,4) \text{ and } (x_2,y_2) = (6,7)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (7 - 4)/(6 - 5)\\\\m = (3)/(1)\\\\m = 3\\\\`

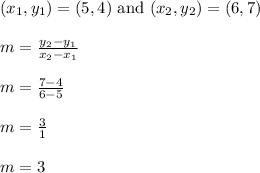
The slope is 3, in which we can think of as 3/1

Each time we move up 3 units (rise), we move to the right 1 unit (run).

------------

Now apply the point-slope formula so we can solve for y

`y - y_1 = m(x - x_1)\\\\y - 4 = 3(x - 5)\\\\y - 4 = 3x - 15\\\\y = 3x - 15+4\\\\y = 3x - 11\\\\`

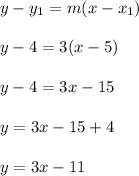
Since the order of the points does not matter, we could use (6,7) in place of (5,4) with the point-slope formula above. You should get y = 3x-11 after isolating y.

This equation has a slope of 3 and y intercept of -11

Two points on this straight line are (0, -11) and (1, -8)

Answer 2

y=3x -11, m=3, b=-11

Step-by-step explanation:

easy