Question

If f(2)=10 and f(7)=14, evaluate f-¹(14)

Answer 1

Answer:
`f^(-1)(14) = 7`

=====================================================

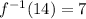
Step-by-step explanation:

Focus only on the f(7) = 14

Apply the inverse function to both sides

`f(7) = 14\\\\f^(-1)(f(7)) = f^(-1)(14)\\\\7 = f^(-1)(14)\\\\f^(-1)(14) = 7\\\\`

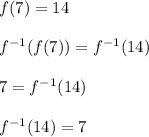
In the third step, I used the rule that
`f^(-1)(f(x)) = x\\\\`

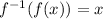
That rule says the inverse function undoes the original function. That's why we get the original input back.

Put another way: The f(7) = 14 says "the input 7 leads to the output 14". When computing the inverse, we go in reverse of this process.

The f(2) = 10 is never used at all. It seems to be filler or a distraction.