Question

Given f(x) and g(x), find f(x)g(x)
and any domain restriction.

Answer 1

`(f(x))/(g(x)) =(x+2)/(x^2+1)` for all x.

Explanation:

As we may see on this expression, it's a fraction of functions. Hence, the only thing that can prevent the expression from giving a defined result is that the denominator equals 0. Therefore, those values of x that make the denominator function equal 0 are going to be the ones than cannot be considered as domains of this fraction of functions. Let's solve equation g(x) when y= 0 to find the values.

`0=x^2+1\\ \\x^2=-1\\√(x^2) =√(-1) \\x=-i`

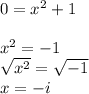
No real solutions where obtained, this means that function g(x) has a domain of all real numbers. Therefore, the function of f(x)/g(x) has a domain of all x values.