Question

Use the divergence theorem to compute the net outward flow of the field f = hx, 2y, zi, and s is the boundary of the tetrahedron in the first octant formed by the plane x y z = 1.

Answer 1

The tetrahedron in question is the set

`T = \left\{(x,y,z)\in\Bbb R^3 ~:~ 0\le x\le1,0\le y\le1-x,0\le z\le1-x-y\right\}`

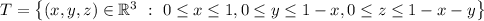
Compute the divergence of the given field.

`\vec f(x,y,z) = \langle x,2y,z \rangle \implies \mathrm{div}(\vec f) = (\partial x)/(\partial x) + (\partial (2y))/(\partial y) + (\partial z)/(\partial z) = 4`

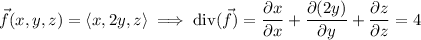
By the divergence theorem, the flux of
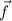`\vec f` across the boundary of
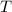`T` is equal to the integral of the divergence over
`T`.

`\displaystyle \iint_(\partial T) \vec f \cdot d\vec S = \iiint_T \mathrm{div}(\vec f) \,dV = 4 \iiint_T dV`

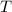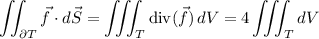
Compute the volume integral. We have

`\displaystyle \iiint_T dV = \int_(x=0)^1 \int_(y=0)^(1-x) \int_(z=0)^(1-x-y) dz\,dy\,dx \\\\ ~~~~~~~~ = \int_0^1 \int_0^(1-x) (1-x-y) \, dy \, dx \\\\ ~~~~~~~~ = \int_0^1 \left((1-x)^2 - \frac{(1-x)^2}2\right) \, dx \\\\ ~~~~~~~~ = \frac12 \int_0^1 (1-x)^2 \, dx \\\\ ~~~~~~~ = \frac12 \int_0^1 (x-1)^2 \, dx \\\\ ~~~~~~~~ = \frac12 \int_(-1)^0 x^2 \, dx \\\\ ~~~~~~~~ = \frac16 (0^3 - (-1)^3) = \frac16`

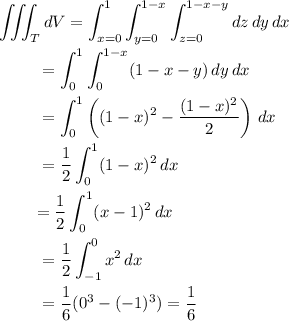
Hence the flux is

`\displaystyle \iint_(\partial T) \ec f \cdot d\vec S = 4 \iiint_T dV = \frac46 = \boxed{\frac23}`

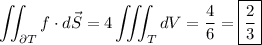
(Thank you stranger for pointing out the error!)