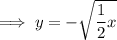Question

which function would be produced by a horizontal stretch of the graph of y = √x followed by a felection in the x-axis

Answer 1

`y=- \sqrt{(1)/(2)x}`

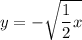
Explanation:

Parent functions are the simplest form of a given family of functions.

Transformations of graphs (functions) is the process by which a function is moved or resized to produce a variation of the original (parent) function.

Transformations

`\begin{aligned} y=f(ax) \implies & f(x) \: \textsf{stretched/compressed horizontally by a factor of} \: a \\ & \textsf{If }a > 1 \textsf{ it is compressed by a factor of}\: a \\ & \textsf{If }0 < a < 1 \textsf{ it is stretched by a factor of}\: a \end{aligned}`

`y=-f(x) \implies f(x) \: \textsf{reflected in the} \: x \textsf{-axis}`

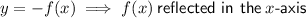
Given parent function:

`y=√(x)`

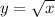
Horizontal stretch:

As this is a horizontal stretch, the x variable should be multiplied by a value between zero and 1:

`\implies y= \sqrt{(1)/(2)x}`

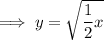
Reflected in the x-axis:

To reflect a function in the x-axis, simply make the function negative:

`\implies y=- \sqrt{(1)/(2)x}`