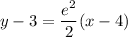I assume the curve has parametric equations
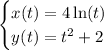
Eliminating the parameter:
Solve for
 .
.
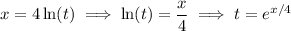
Substitute this into
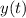 .
.

Compute
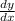 and evaluate it at (4, 3) (that is, with
and evaluate it at (4, 3) (that is, with
 ) to find the slope of the tangent line at that point.
) to find the slope of the tangent line at that point.

Use the point-slope formula to get the equation of the line.

Without eliminating the parameter:
Use the chain rule to compute
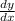 .
.
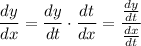
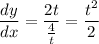
When
 , we have
, we have
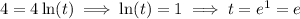
and so at (4, 3), the slope of the tangent is
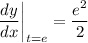
Then using the point-slope formula, the tangent line's equation is again