Obtain two vectors that lie in the plane containing the triangle.
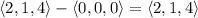

Compute their cross product to get the normal vector to the plane.
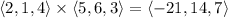
Now, the angle
 made by
made by
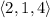 and
and
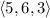 is such that
is such that
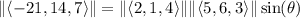
and this expression is exactly the area of the parallelogram spanned by the two vectors. Cut this in half to get the area of the triangle in question.
We have
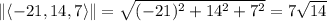
and so the area of
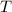 is 7√14/2.
is 7√14/2.