Part A
Answer: sample space is {1,2,3,4,5,6}
Reason: It is the set of possible outcomes, i.e. possible die rolls.
=======================================================
Part B
Answer: 1/6
Reason: There is one face showing "5" out of 6 faces total.
=======================================================
Part C
Answer: 1/2
Reason:
Half of the numbers are even.
Three numbers are even out of 6 total. So 3/6 = 1/2.
=======================================================
Part D
Answer: 2/3
Reason:
The outcomes we want are {3,4,5,6} which are 4 outcomes out of 6 total. Therefore we get 4/6 = 2/3 as the probability of getting something larger than 2.
=======================================================
Part E
This is what the probability model looks like
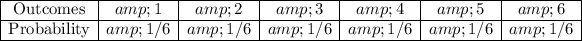
The first row deals with the sample space. Refer to part A to see the sample space. It's the list of all possible outcomes on the number cube.
In the bottom row is the probability for each outcome. Assuming a fair number cube, each probability should be 1/6, since we have 1 side out 6 total. Each side has equal chance of showing up on any given roll.
Notes:
- Everything in the bottom row adds to 1
- The term "probability model" is interchangeable with "probability distribution".
- This distribution is discrete because of the finitely many outcomes
=======================================================
Part F
Answer: Uniform
Reason:
A uniform probability distribution has each outcome with the same chances of it happening. That probability being 1/6 in this case.
Another example of a uniform distribution would be a coin toss. Each outcome (heads or tails) has probability 1/2.
Think "uniform" as in "same", in that every solider in the army wears the same uniform.
=======================================================
Part G
Answer: 2/3
Reason:
The multiples of 3 on the number cube are {3,6}
The non-multiples of 3 are {1,2,4,5}. We have 4 outcomes we want out of 6 total, so we get to the answer of 4/6 = 2/3. Interestingly this is the same fraction as part D.