Answer: population mean μ = 37.40 mm; population std dev σ ≈ 7.57 mm
Explanation:
The first group of numbers is the set of ranges for the categories (or 'classes') we will use. The second group of numbers is how many observations (frequency) for each category.
If the categories were just single numbers, we would get the total category values by multiplying the frequency times the category value. But the categories are each a range of values. What we do here is we take the midpoint of each range, and use that.
So we have range midpoint values of 22, 27, 32, 37, 42, 47, and 52.
We get the population mean by multiplying each class midpoint times its frequency, and then summing up all the products, and then dividing by the total number of observations, 'N'.
N = 6+10+18+25+22+15+4 = 100
For frequency * class midpoint, we have ...
6 * 22 = 132
10 * 27 = 270
18 * 32 = 576
25 * 37 = 925
22 * 42 = 924
15 * 47 = 705
4 * 52 = 208
If we add these up, we get 3740
(a.) population mean μ = 3740/N = 3740/100 = 37.4 mm
The population standard deviation is the square root of the population variance, so we must get the variance first.
variance is the average of the squared differences from the mean.
We take each data point (midpoint of its class), subtract the mean, then square that difference. Then we multiply that squared difference by the frequency for that class. Then we add all those products together.
This takes some time to do manually, but here goes. ( If you have Microsoft Excel, the program can be used to do a lot of this.)
For Class 1 (midpt 22): 6 * (37.4 - 22)^2 = 1422.96
For Class 2 (midpt 27): 10 * (37.4 - 27)^2 = 1081.60
For Class 3 (midpt 32): 18 * (37.4 - 32)^2 = 524.88
For Class 4 (midpt 37): 25 * (37.4 - 37)^2 = 4.00
For Class 5 (midpt 42): 22 * (37.4 - 42)^2 = 465.52
For Class 6 (midpt 47): 15 * (37.4 - 47)^2 = 1382.40
For Class 7 (midpt 52): 4 * (37.4 - 52)^2 = 852.64
If we add all the products together, we get 5,734.00
Divide by N = 100
5734/100 = 57.34
The population variance is 57.34 mm squared
The population standard deviation is Greek letter sigma (lower case) σ and is the square root of the variance, so
(b.) σ =
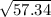 ≈ 7.57 mm
≈ 7.57 mm
Notice that when we get to the std dev, we are back at the original unit of measure, not its square
I hope this helps.