Answer:
Explanation:
Given a system of equation
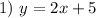

Substitute the 2) equation for the y value of the 1) equation

Subtract [ 2x + 5 ] on both sides
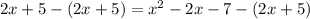
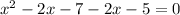
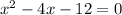
Cross multiply the equation


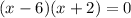
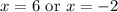
Since there are 2 x values, this represents that there are
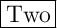 intersecting points
intersecting points
----------------------------------------------------------------------------------------------------------
The following is EXTRA information for the question if you need to find the points of intersection
Substitute the x values into one of the equations to find the y value
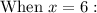
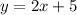
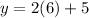
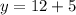
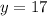
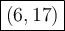
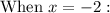
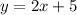
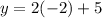
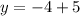
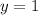

Graph the equations to check the solutions
Please refer to the attachment below for the graph