Question

A ball of mass 0.15kg is kicked against a ridge vertical with horizontal velocity of 50m/s. If it rebounded with a horizontal velocity of 30m/s, calculate the impulse of the ball to the wall​

Answer 1

So, the impulse of the ball to the wall is -12 N. It have same meaning to 12 N in opposite direction with its initial movement.

Introduction

Hi ! In this ocassion, I will help you to solve the question about impulses. Impulse also relate to momentum, where the amount of impulse will cause the difference (indicated in units of direction) velocity when an object move. Impulses that have opposite direction to the original direction will have a negative value.

Formula Used

Impulse is the result of a change in momentum, so it can be expressed in this formula :

`\sf{I = \Delta p}`

`\boxed{\sf{\bold{I = m (v' - v_0)}}}`

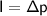
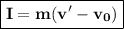
With the following condition:

• I = impulse (N.s)
• m = mass of the object (kg)
• 
  `\sf{v'}` = final speed after collision (m/s)
• 
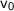  `\sf{v_0}` = initial speed before collision (m/s)

Problem Solving

Tips:

• We will use the starting point of the ball as a reference for the direction of ball's velocity. This is because what is being asked is the impulse of the ball to the wall not the impulse of the wall to the ball. But still, the value is the same.

We know that :

• m = mass of the balls = 0.15 kg
• 
  `\sf{v'}` = final speed of the balls = -30 m/s (30 m/s at the opposite direction from initial speed).
• 
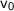  `\sf{v_0}` = initial speed of the balls = 50 m/s

What was asked ?

• I = impulse the ball to the wall = ... N.s

Problem solving :

`\sf{I = m (v' - v_0)}`

`\sf{I = 0.15 (-30 - 50)}`

`\sf{I = 0.15 (-80)}`

`\boxed{\sf{I = -12 \: N.s}}`

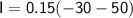
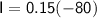
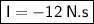
Conclusion

So, the impulse of the ball to the wall is -12 N. It have same meaning to 12 N in opposite direction with its initial movement.