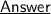
Let's solve ~
Here, for each value of x, we have a unique value of y. so we can conclude that it's a function.
or
Draw vertical lines all over the graph, if the vertical lines cut the curve once then it is a function, and if more than once then it isn't a function.
Since the lines cut the curve once everytime, it is a function
Domain :
It's a continuous function that extends to infinity on both sides, so it's domain is :
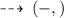
Range :
It's a parabolic function with least value of y = -3 and extends to infinity upwards.
so it's range is :
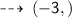
Y - intercept :
The point where it cuts the y - axis is (0 , 1), so y - intercept = 1
Zeros :
The values of x at which the function cuts the x - axis are the zeros of the given function.
[ In the given graph t isn't specified properly at what points it cut x - axis, but the range in which they lie are : 1st zero : between 0 and 1, 2nd zero : between 3 and 4. ]
So, the approximate values are : 0.25 and 3.75
Value of F (1) = ?
If we plug the x - coordinate as one, it's y - coordinate will be -2 on the given curve.