Question

determine algerbraically if the following functions are even,odd, or neither. if even or odd, state the symmetry

Answer 1

`{ \qquad\qquad\huge\underline{{\sf Answer}}}`

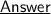
The given function is an even function, as the polynomial has degree 6, and all the terms in the polynomial has even powers

`{ \qquad \sf  \dashrightarrow\:f(-x)=(-x)⁶-2(-x)² + 3}`

`{ \qquad \sf  \dashrightarrow \: f(-x) = x⁶ - 2x² + 3}`

`{ \qquad \sf  \dashrightarrow \: f(-x) = f(x)}`

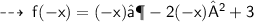
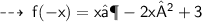
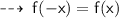
As the values for " -x " and " x " are same, since they have even powers.

And if we observe the function properly,

`\qquad \sf  \dashrightarrow \: ( {x}^(6) - 2 {x}^(2) ) + 3`

[ graph of x⁶ - 2x² is symmetric about y - axis, and if we add 3, it shifts 3 units upside so there's no change to symmetry. ]

Conclusion : The graph is symmetric about y - axis.