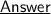
The given function is :
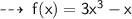

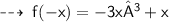
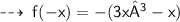
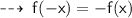
Hence, it's an odd function.
Also, the polynomial has odd powers, there is different value of y for each and every value of x, even for numbers and their additive inverse. and there will be symmetry in it about (0 , -3)
Therefore it's an odd function.