Answer:
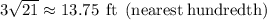
Explanation:
The given scenario can be modeled as a right triangle, where the distance from the foot of the ladder to the base of the building is the base of the triangle, and the ladder is the hypotenuse of the triangle.
To find the height of the building, and therefore the height of the triangle, use Pythagoras Theorem.
Pythagoras Theorem
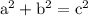
where:
- a and b are the legs of the right triangle.
- c is the hypotenuse (longest side) of the right triangle.
Given:
- a = height
- b = base = 6 ft
- c = hypotenuse = 15 ft
Substitute the given values into the formula and solve for a:
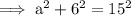
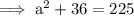
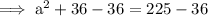
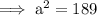
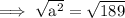
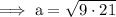
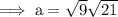
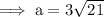
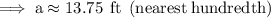
Therefore, the height of the building is 13.75 ft (nearest hundredth).