Answer:
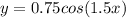 or
or
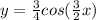 .
.
Explanation:
1. Identify whether the function is sin or cos.
This function is a function of the cosine (cos), because it's value for x= 0 isn't 1. If it was a sinus function, it's value for x= 0 would be 0.
2. Find "a".
"a" is the value that tells us the amplitude of the function, its initial height . As you may notice on the graph, the initial height of this graph is 0.75. Hence, a= 0.75.
Note. If the function started on height y= -0.75, then a= -0.75.
3. Find "b".
"b" tells us what the period of the fuction is. The period is just the lenght of the wave before it starts repeating its pattern again. Let's use the following fomula to find b:
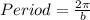
As you can tell from the graph, the graph has a length of
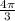 before it starts repeating the pattern again. Hence, period is
before it starts repeating the pattern again. Hence, period is
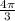 . To obtain b, solve the equation for b:
. To obtain b, solve the equation for b:
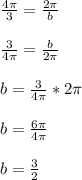
4. Form the equation.
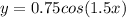 .
.
-------------------------------------------------------------------------------------------------------
Check out the attached image to better understand the variables of a trigonometric function on the cartesian plane. This image is a fragment from the book "Precalculus, 7th ed.", from author James Stewart.